Hashing
Trong quá trình tham gia vào công việc phát hiện và xác định dữ liệu phù hợp thông qua key và ID, một nghiên cứu đã sử dụng thuật toán Hashing. Hashing đóng vai trò quan trọng trong việc mở rộng chức năng của hệ thống, bao gồm việc phát hiện lỗi, quản lý bộ nhớ cache, mã hóa và tra cứu dữ liệu. Bằng cách tích hợp các khóa phù hợp, hàm Hashing giúp đảm bảo tính chính xác của các giá trị được truy xuất và sử dụng trong quá trình này.

Hàm này cũng có thể được sử dụng như một định danh duy nhất cho các tập dữ liệu nhất định và các phép tính toán cho phép người dùng tạo ra các giá trị dữ liệu không trùng lắp. Thông thường nó được áp dụng trong các bộ định tuyến để lưu trữ địa chỉ IP.
Search Algorithms
Thuật toán tìm kiếm thường được áp dụng cho cấu trúc dữ liệu tuyến tính hoặc đồ thị. Phương pháp tìm kiếm tuyến tính, còn được biết đến là tìm kiếm nhị phân, giúp nhà phát triển thực hiện tìm kiếm một cách hiệu quả trên các tập dữ liệu đã được sắp xếp, với thời gian chạy phức tạp O(log N). Thuật toán này hoạt động bằng cách chia nhỏ danh sách ban đầu thành hai phần, lặp đi lặp lại quá trình này cho đến khi phần tử được tìm thấy. Tìm kiếm nhị phân thường được sử dụng để phát hiện và sửa lỗi trong quá trình gỡ lỗi, chẳng hạn như trong git bisection.
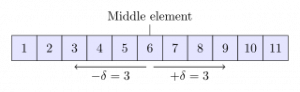
Các thuật toán này còn được biết đến với chức năng là Chiều sâu/Chiều rộng Tìm kiếm Đầu tiên, nó cho ta cấu trúc dữ liệu là một biểu đồ tròn hoặc hình cây đã bật chức năng tìm kiếm, xác định các tập dữ liệu cần thiết trong mô hình cây ngang. BFS rất phổ biến trong các công cụ tìm kiếm, cũng được sử dụng để xây dựng các bot trong AI hay định vị các con đường ngắn nhất giữa hai thành phố.
Thuật toán sắp xếp (Sort Algorithms)
Các thuật toán sắp xếp thường được các nhà phát triển dùng để đặt dữ liệu theo cách có tổ chức. Trong thuật toán QuickSort, các thành phần dữ liệu được so sánh với nhau để xác định thứ tự tương ứng của chúng.
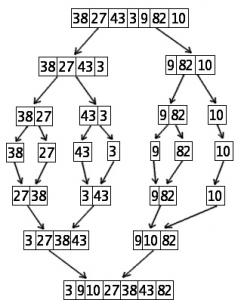
Nó có độ phức tạp thời gian của O(nLogn) để thực hiện so sánh. Tuy nhiên, Radix Sort là một kỹ thuật nhanh hơn QuickSort vì nó sắp xếp các phần tử trong một mô hình tuyến tính với độ phức tạp thời gian O(n). Tính đơn giản của thuật toán này làm cho nó được ưa chuộng. Các thuật toán sắp xếp khác bao gồm Sắp xếp hợp nhất, Sắp xếp nhóm và Sắp xếp đếm.
Thuật toán lập trình động (Dynamic Programming Algorithms)
Lập trình động thường là một hàm giải quyết vấn đề phức tạp liên quan đến trí tuệ bằng cách tách các vấn đề thành các bài toán con nhỏ hơn, giải quyết chúng sau đó xây dựng trở lại thành vấn đề phức tạp với bộ nhớ của các kết quả nhỏ hơn để đưa ra câu trả lời cho vấn đề phức tạp ban đầu.
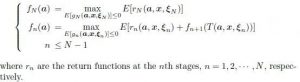
Lập trình động có khả năng tích hợp để ghi nhớ, cho phép lưu trữ các ký ức về các vấn đề đã giải quyết trước đó. Nếu lần tiếp theo vấn đề ấy lại xuất hiện thì nó sẽ được giải quyết nhanh hơn nhiều.
Phân tích liên kết (Link Analysis)
Phân tích liên kết là một công cụ quan trọng trong lĩnh vực mạng, giúp phân tích mối quan hệ giữa các thực thể khác nhau trong một miền cụ thể, đặc biệt quan trọng đối với các công cụ tìm kiếm. Thuật toán của nó sử dụng biểu diễn đồ họa và ma trận phức tạp để xác định mối liên hệ giữa các phần tử trong miền đó. Phân tích liên kết có ứng dụng phổ biến trong các dịch vụ tìm kiếm như Google, cũng như trên các nền tảng mạng xã hội như Facebook, Twitter, nơi mà việc tìm kiếm và mở rộng mạng lưới quan hệ được coi trọng.
Phép toán Mô-đun (Modulo Arithmetic Algorithms)
Nhiều thuật toán mã hóa, mặc dù ban đầu phức tạp, nhưng khi áp dụng trên nền số học mô đun, chúng trở nên đơn giản hơn đáng kể. Trong số học mô đun, chúng ta chỉ xử lý các số nguyên và thực hiện các phép toán cơ bản như cộng, trừ, nhân và chia. Điều đặc biệt là trong số học mô đun, mọi hoạt động liên quan đến các số nguyên dương, cụ thể là modulo.
Ví dụ:
- Thuật toán Euclide cơ bản và mở rộng
- Phương trình hoàn hảo của Euler
- Lũy thừa mô đun
- Tính nghịch đảo theo mô đun
- Định lý số dư của Trung Quốc
- Định lý số dư của Trung Quốc và thực thi tính nghịch đảo của mô đun
Thuật toán xâu ký tự và phân tích cú pháp (String Matching and Parsing Algorithms)
Quy trình tạo xâu tương ứng luôn quan trọng đặc biệt đối với miền và phần tử mạng. Thuật toán xâu ký tự này sẽ phát huy khả năng tối đa trong các tình huống mà các xâu phải khớp trong một chuỗi dài hoặc khi xác nhận chuỗi bằng cách phân tích cú phápqua giới hạn được xác định trước. Các thuật toán này thường được sử dụng trong phát triển web cho URL.
Thuật toán biến đổi Fourier (Fourier Transform Algorithms)
Biến đổi Fourier hay Biến đổi Fourire nhanh là những thuật toán đơn giản nhưng rất mạnh. Chúng được sử dụng để chuyển đổi tín hiệu từ miền thời gian sang miền tần số và ngược lại. Toàn bộ các mạng kỹ thuật số như Internet, WiFi, điện thoại, máy tính, bộ định tuyến, vệ tinh, sử dụng thuật toán này theo để vận hành. Đây là những thuật toán bắt buộc phải biết nếu bạn chuyên sâu về mảng điện tử, điện toán hoặc viễn thông.
Thuật toán các tập không giao nhau (Disjoint Sets)
Thuật toán tập không giao nhau chức năng như một công cụ hỗ trợ trong việc biểu diễn nhiều tập hợp riêng biệt trong một mảng. Mỗi phần tử trong mảng đại diện cho một phần của một tập hợp cụ thể. Cấu trúc này được sử dụng trong các thuật toán đồ thị hoặc trong việc phân đoạn hình ảnh để biểu thị mối liên kết giữa các phần tử.
Hệ số tích phân (Integer Factorization)
Thuật toán lũy thừa số nguyên là một thuật toán toán cung cấp hướng dẫn từng bước về cách lấy các thừa số nguyên tố của một số tổng hợp. Thuật toán này giải quyết các vấn đề phức tạp trong các nền tảng mã hóa yêu cầu bạn phải giải quyết các số nguyên phức hợp lớn.